小數乘法算理的秘密，還可以這樣告訴孩子……

學習小數乘小數時，幾個不同版本的教材都同時把重點放在探究乘數和積的關系上。借助乘數和積的關系變化，幫助學生認識小數乘法轉化為整數乘法進行運算的一般步驟，“積的變化規律”由此貫通了小數乘小數算理表征的始終（如圖1）。

（圖1）

我們還可以基于學生已有的知識經驗，從不同的理解角度探尋小數乘法算理的秘密：

思考一：除了積的變化規律，還可以怎樣幫助學生理解小數乘法？

北師大版教材提供兩個學生可能的思路，為學生創設于理解的基礎上探索算法的學習過程。

方法一：借助單位換算，利用長度單位及面積單位之間的關系，將小數乘法轉化為整數乘法，進而得出0.3×0.2＝0.06（如圖2左）。

方法二：通過面積模型，幫助學生于直觀中得出結果（如圖2右）。

（圖2）

方法三：巧用小數的意義和運算律。在如下（圖3）推理過程中，既可以幫助學生理解0.3×0.2的計算道理，其實就是在算有幾個0.01這樣的計數單位，同時能清楚地看到0.01這個計數單位是由“0.1×0.1”得來的。

（圖3）

按這個角度來分析存在著一個問題：0.1×0.1為什么等于0.01？這也是小數乘法的算理難點。

在查閱資料的過程中，我們發現有的教材（比如臺灣康軒版）在小數乘法的學習中，首先編排“0.1×0.1”單位小數相乘的學習內容，并將分數乘法的學習安排在小數乘法之前（如圖4），借此幫助學生理解“0.1×0.1＝0.01”的道理。

（圖4）

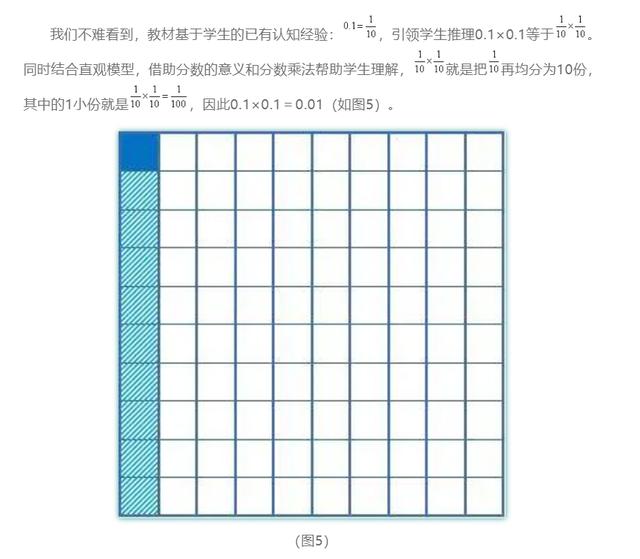
思考二：不同的理解方法之間又有什么樣的關系？

再聯系單位換算和直觀的百格圖視角，其道理也是一樣的。

因此，不管從哪一個角度來分析推理，其計算的道理都是相通的。

0.3×0.2都是在算（3×2）個（0.1×0.1）是多少，也就是有幾個0.01這樣的計數單位（如圖7）。

（圖7）

帶著這個視角回顧乘法的算理（如圖8）。

（圖8）

比如整數乘法中：

3×2表示（3×2）個1，其實就是（3×2）個（1×1）

30×2表示（3×2）個（10×1）

30×20表示（3×2）個（10×10）

小數乘法中：

0.3×2表示（3×2）個（0.1×1）

0.3×0.2表示（3×2）個（0.1×0.1）

分數乘法也一樣：

……

因此，追根究底，小數乘法的計算道理和整數乘法、分數乘法都是一致的，都是在算有幾個這樣的計數單位。

- END -

來源：明師之道。

作者：黃偉華，本科學歷，高級教師，福建省晉江市心養小學教科室副主任。